Cache overview

contents: 0-1. CA Intro

Memory hierarchy

Locality

Temporal locality

- Items accessed recently are likely to be accessed again soon

Spatial locality

- Items near those accessed recently are likely to be accessed soon

Memory structure

SRAM (cache memory attached to CPU)

- Fastest (o.5ns ~ 2.5ns)

- most expensive

- smallest

DRAM (main memory)

- Faster (50ns ~ 70ns)

- more expensive

- smaller

Disk (HDD, SSD)

- Slowest (5ms ~ 20ms)

- cheapest

- largest

Use hierarchy

Copy recently accessed (and nearby) items from disk to smaller DRAM memory
Copy more recently accessed (and nearby) items from DRAM to smaller SRAM memory

Term

Block

- The minimum unit of information

- It can be either present or not present in a cache

Hit

- Accessed data is present

- Hit ratio: # of hits / # of accesses

Miss

- Accessed data is absent

- Block is copied from lower level (Additional time taken)

- Miss ratio: # of misses / # of access (= 1 - hit ratio)

Direct mapped cache

Each memory location can be mapped directly to exactly one location in the cache

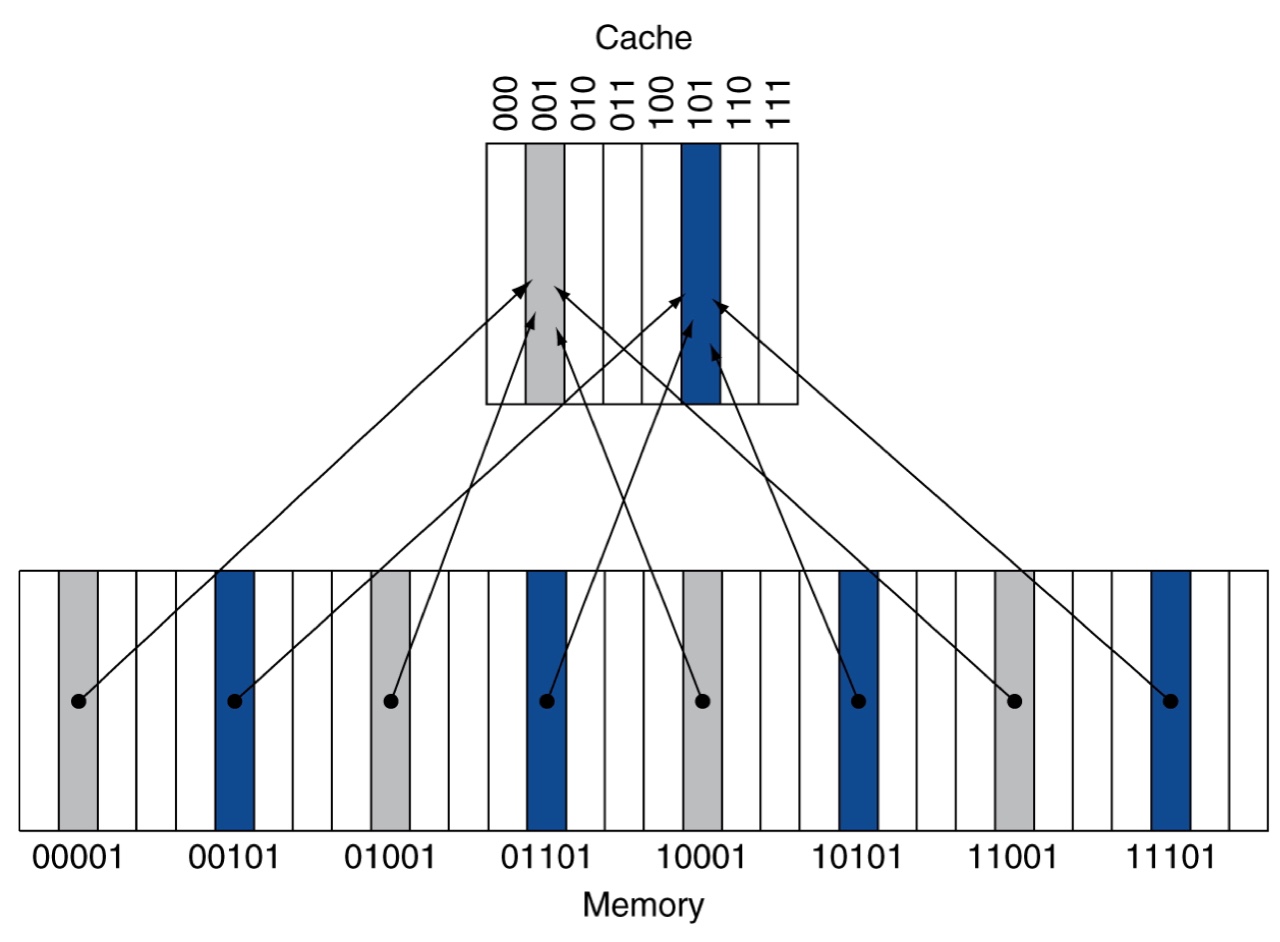
Cache address = (Block address) modulo (# of blocks in cache)
Num of blocks in cache is power of 2 (e.g., 2, 4, 8, 16, 32, ...)
The cache address is determined by the low-order bits of block address
Tags contain the address information of the data (the high-order bits of the address)
To avoid using meaningless information, add a valid bit for each cache block

- Valid bit = 1 (the cache block contains valid information)

- Valid bit = 0 (the cache block contains invalid information)

- Initially, the valid bits of all cache blocks are set to 0

Cache address

32-bit addresses
num of cache blocks: $2^n$ blocks (the lowest n bits of the block address are used for the index)
Block size: $2^m$ words ( $2^{m+2}$ bytes)

- m bits are used for the word within the block, 2 bits are used for the byte within the word

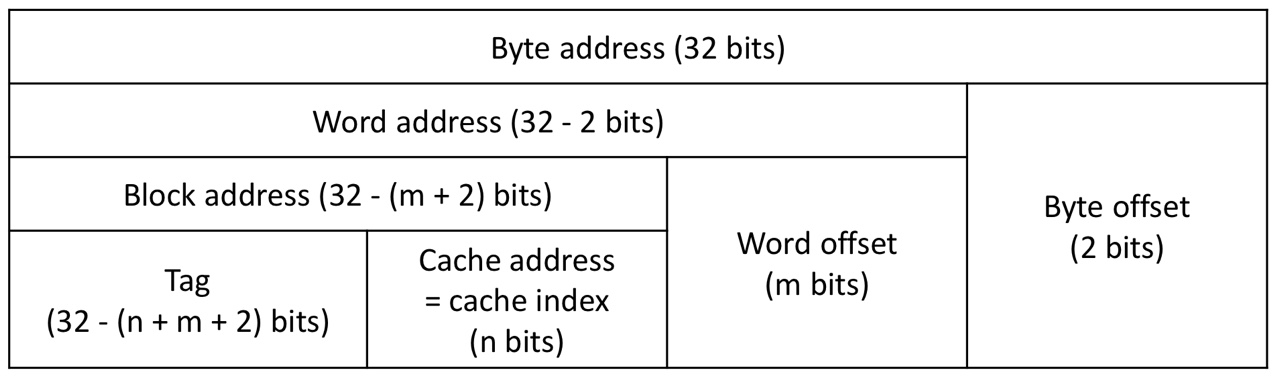
Cache size

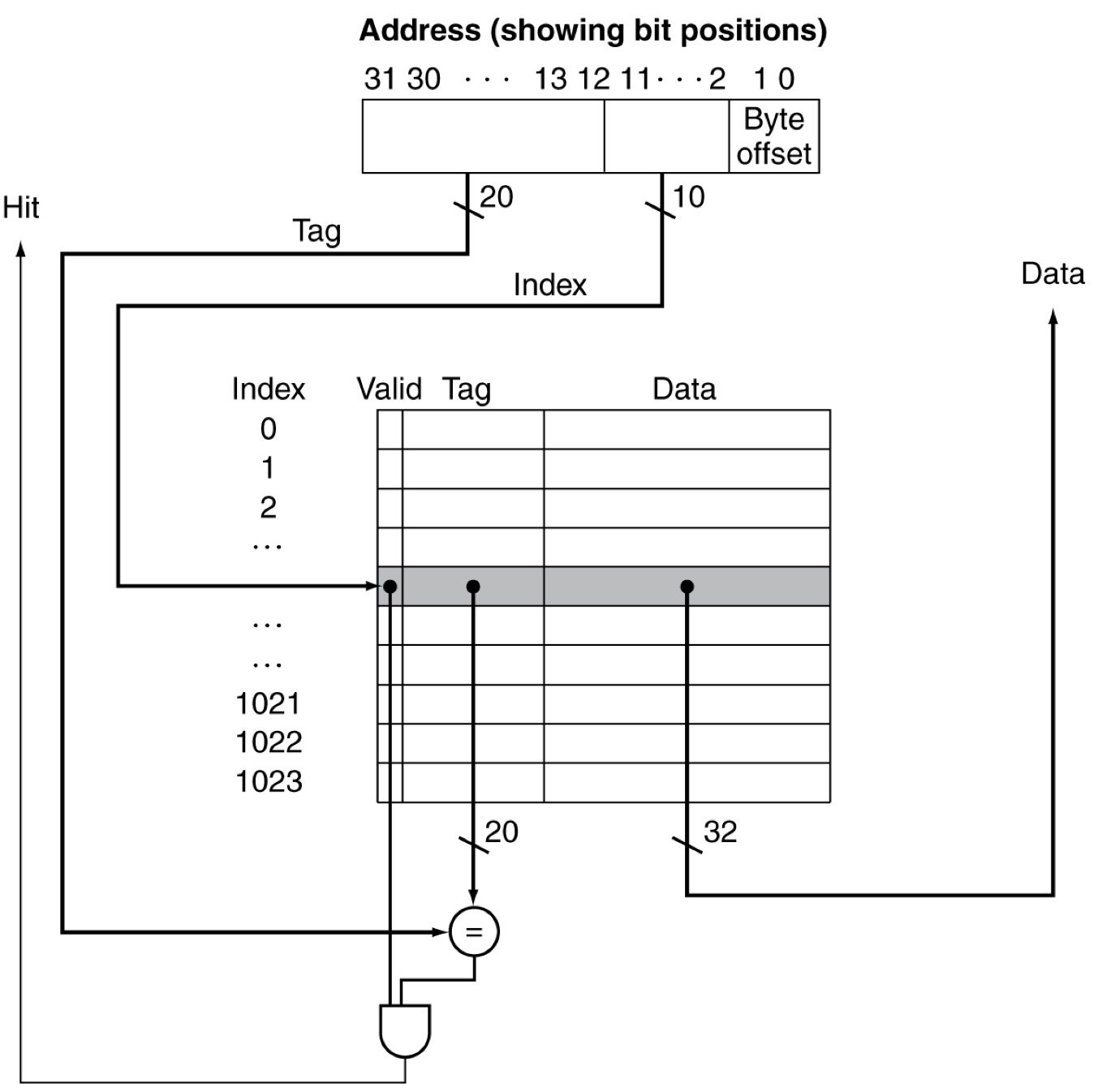
Cache size

= Cache table size

= Num of cache block $\times$ (valid bit length + tag length + block size(data length))

Practice 1

32-bit addresses
Num of cache blocks: $2^{10}$ blocks
Block size: $2^0$ words ( $2^2$ bytes)

Cache size

= $2^{10} \times (1 + (32 - (10 + 0 + 2)) + 32)$

= $2^{10} \times 53$ bits

Practice 2

32-bit addresses
Num of cache blocks: 64 blocks
Block size: 4 words

Cache size

= $2^{6} \times (1 + (32 - (6 + 2 + 2)) + 128)$

= $2^{6} \times 151$ bits

More about

If we increase the size of blocks, this may help reduce miss rate due to spatial locality
But, Larger blocks -> a smaller number of cache blocks -> more competition -> increased miss rate
Increased miss penalty (the time for copying from lower level)

Handling cache misses

On cache hit, CPU proceeds normally. (requiring 1 clock cycle

But, on cache miss, the control unit of the CPU

Step 1: stalls the CPU pipeline
Step 2: copies a block from the next level of hierarchy (e.g., memory)
Step 3: does the stalled task

- Restarts instruction fetch (IF stage)
if the cache miss happened when fetching an instruction from the instruction memory

- Completes data access (MEM stage)
if the cache miss happened when loading data from the data memory

Handling writes

When will the newly-updated data in the cache be written to the lower-level memory (e.g., main memory)

Write-through: Update both cache and lower-level memory at the same time
Write-back: Just update cache

- Keep track of which block is dirty (used)

- When a dirty block is replaced, write it back to the lower-level memory

	Pros	Cons
Write-through	- Consistency between cache and memory is guaranteed - Easy to implement	- Slow write speed
Write-back	- Fast write speed (if there is no replacement)	- Consistency between cache and memory is not guaranteed - Complex to implement

Write-through with write buffer

To reduce the delay of write operations on the write-through method,
we can use a write-buffer (much faster to access than memory)

A write buffer folds data waiting to be written to lower-level memory

- Step 1: Update both cache and write buffer

- Step 2: The processor continues the program execution without waiting

- The memory takes the updated data from the write buffer

If the buffer is full, the processor must stall until there is an empty position

The write buffer can be also used to improve the performance of write-back

If all the blocks in cache are dirty

Handling write misses

If there is no requested block in the cache, it causes write misses

Write-allocate

- First, fetch the block to cache

- And then, handle the write operation

Write around

- Just update the portion of the block in lower-level memory, but not put it in cache

- It is good when we need to initialize memory space

Real-world example

Embedded MIPS processor with 12-stage pipeline

Split cache: I-cache (for instructions) and D-cache (for data)
Each 16KB: 256 blocks $\times$ 16 words per block

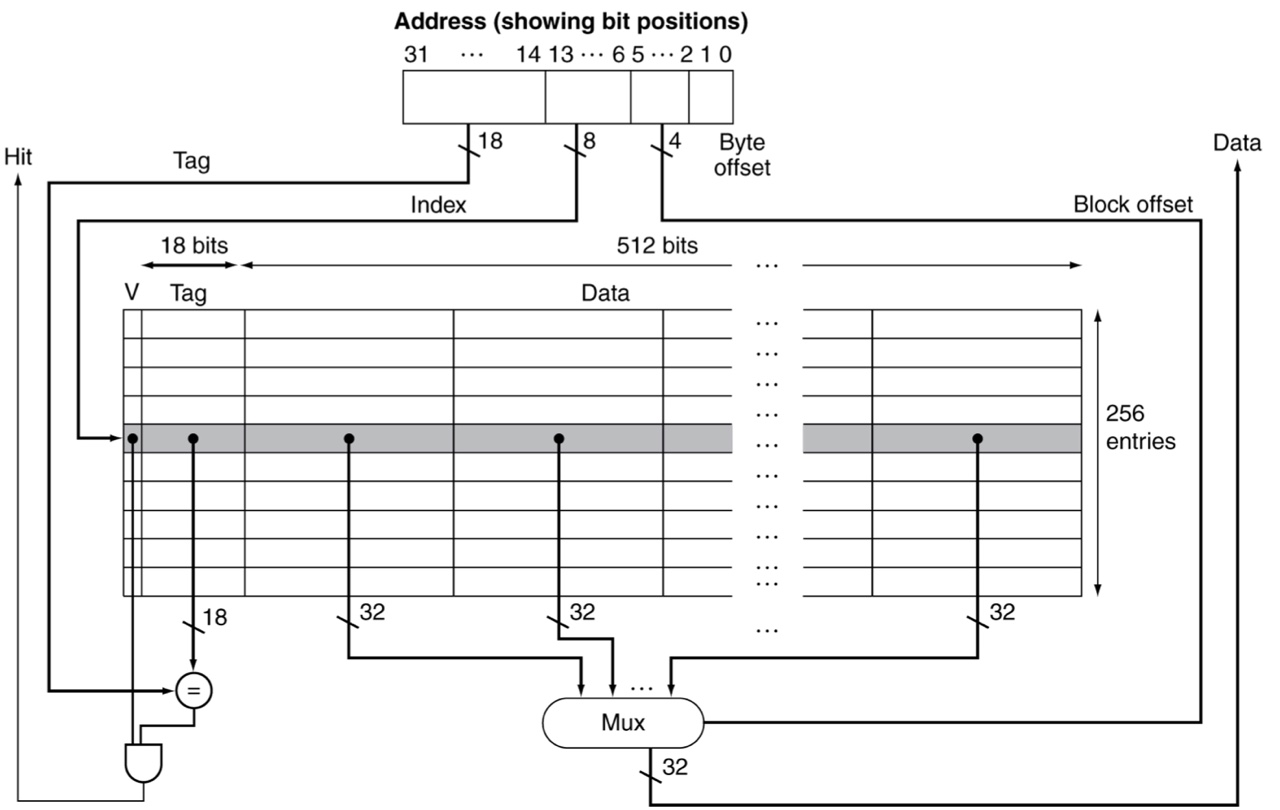
Cache performance

CPU time = clock cycle $\times$ clock period

= (CPU execution clock cycles + memory-stall clock cycles) $\times$ clock period

CPU execution clock cycles

- The clock cycles that CPU spends executing the program

- Cache hit time is included

Memory-stall clock cycles

- The clock cycles that CPU spends waiting for the memory access

- Mainly from cache misses

Memory-stall clock cycles

Simplifying assumption: the read and write miss penalties are the same

Num of memory accesses $\times$ Miss rate $\times$ Miss penalty

= Num of misses $\times$ Miss penalty

In MIPS, we have two different cache (instruction (I-cache) and data (D-cache))

Num of memory accesses $\times$ Miss rate $\times$ Miss penalty

= Num of instruction memory access $\times$ I-cache miss rate $\times$ I-cache miss penalty

$+$ Num of data memory access $\times$ D-cache miss rate $\times$ D-cache miss penalty

Practice 1

Base CPI (on cache hit) = 2
Instruction-cache miss rate = 2%
Data-cache miss rate = 4%
Miss penalty = 100 cycles
Load & stores are 36% of instructions

Miss-stall clock cycles (when there are I instructions)

For instructions: I $\times$ 0.02 $\times$ 100 = 2 $\times$ I
For data: I $\times$ 0.36 $\times$ 0.04 $\times$ 100 = 1.44 $\times$ I

CPU time

Actual CPU time: (2 $\times$ I + 2 $\times$ I + 1.44 $\times$ I) $\times$ clock period = 5.44 $\times$ I $\times$ clock period
Ideal CPU time: (no cache misses = perfect cache): 2 $\times$ I $\times$ clock period

\frac{Ideal\;performance}{Actual\;performance} = \frac{Actual\;CPU\;time}{Ideal\;CPU\;time} = \frac{I \times actual\;CPI \times clock\;period}{I \times ideal\;CPI \times clock\;period} \\ = \frac{Actual\;CPI}{Ideal\;CPI} = \frac{5.44}{2}

"The performance with the perfect cache is better by 2.72"

Practice 2

Suppose the processor is made faster, but the memory system is not

Base CPI (on cache hit) = 2 -> 1
Instruction-cache miss rate = 2%
Data-cache miss rate = 4%
Miss penalty = 100 cycles
Load & stores are 36% of instructions

	Memory-stall clock cycle	Memory-stall CPI
For I-cache	2 $\times$ I	2
For D-cache	1.44 $\times$ I	1.44
	CPU time	CPI
Actual	4.44 $\times$ I $\times$ CP	4.44
Ideal	1 $\times$ I $\times$ CP	1

"The performance with the perfect cache is better by 4.44"

But the gap between actual and ideal case is same as 3.44