MIPS memory allocation & addressing

contents: 0-1. CA Intro

MIPS memory allocation

To avoid the overlap for managing memory, we use stack, heap, and static space.

Stack

During the procedure call, both registers and local variables are stored on stack.

We call the segment of the stack activation record or procedure frame

The frame pointer ($fp) points to the first word of the frame
During the execution of a procedure, $fp is stable. So, it is used to reference variables

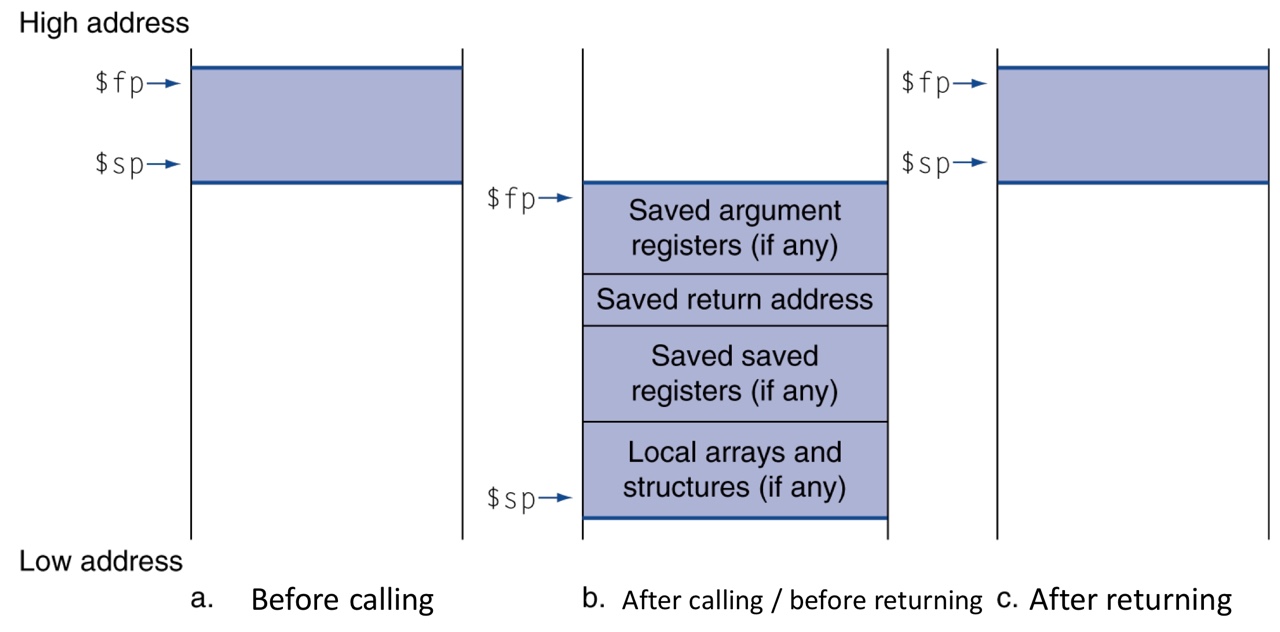
Activation record

- managed in a stack from high address to low address

Heap

Dynamically-allocated data

- managed in a heap from low addresses to high addresses

Static space

Global variables

- assigned a fixed address

- statically allocated

- all reference to a global variable point to the same object

- it cannot be stored in an activation record

Code & Data in memory

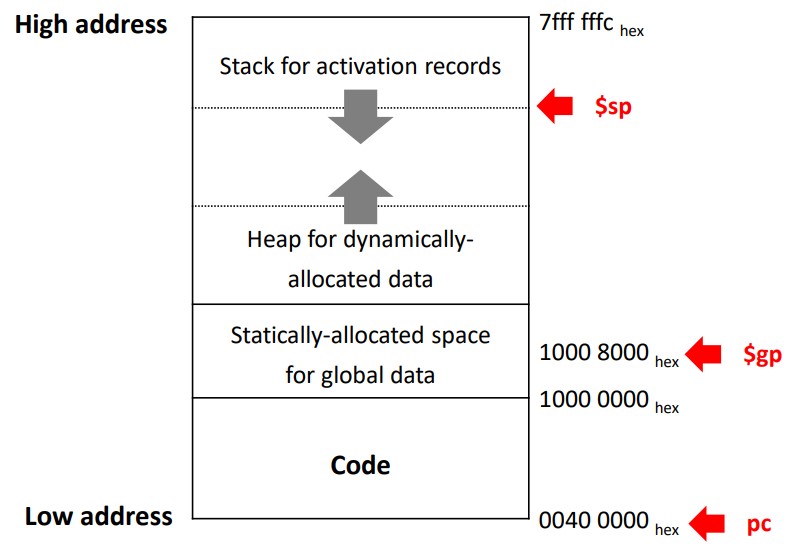
These addresses are only a software convention, and not part of the MIPS architecture.

The stack pointer ($sp) is initialized to 7fff fffc $_{hex}$ and grows down toward the data segment
At the other end, the program code starts at 0040 0000 $_{hex}$

- From 0000 0000 $_{hex}$ to 0040 0000 $_{hex}$ is just reserved

The static data starts at 1000 0000 $_{hex}$
The global pointer ($gp) is set to an address to make it easy to access data, and initialized to to 1000 8000 $_{hex}$ so that it can access fromm 1000 0000 $_{hex}$ to 1000 ffff $_{hex}$ using the positive and negative 16-bit offsets from $gp
Dynamic data is grows up toward the stack in an area called heap

Addressing mode

After we decode instructions, we will perform corresponding tasks.

At this time, we need to access data or instructions which can be stored in instructions, registers or memory.

1. Immediate addressing (with immediate operands)

by decoding instructions, we can get data directly
last 16 bits are used to represent data
the operand is 16 bits of the instructions
don't need to access other place

Supporting 32-bit constants

Sometimes, we need to use a 32-bit constants

lui instruction

- transfers the 16 bit immediate constant field value into the leftmost 16 bits of the register

- fills the lower 16 bits with 0s

ori instruction

- fills the lower 16 bits with given data

2. Register addressing (with register operands)

use 5 bits to represent register number from 0 to 31

- because there are 32 registers

work like a pointer

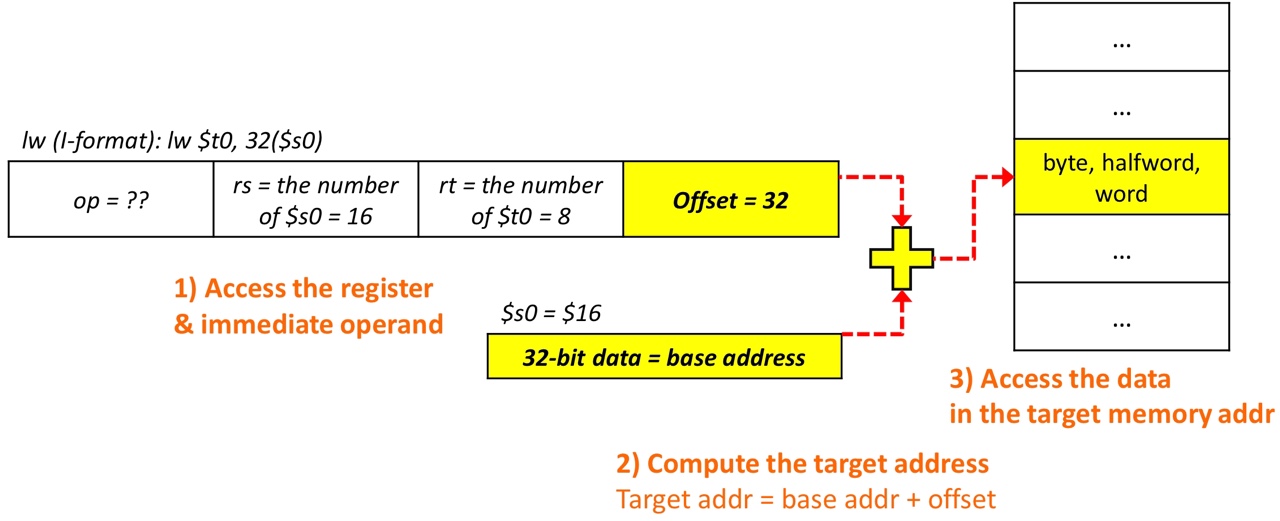
3. Base addressing (with data transfer instructions)

rs points base address, and last 16 bits represent offset
16 bits can represent from -2 $^{15}$ to 2 $^{15}$ -1

- 2 $^{15}$ = 8000 $_{hex}$

- $gp always points 1000 8000 $_{hex}$ which means that, with offset it can access every statically-allocated space

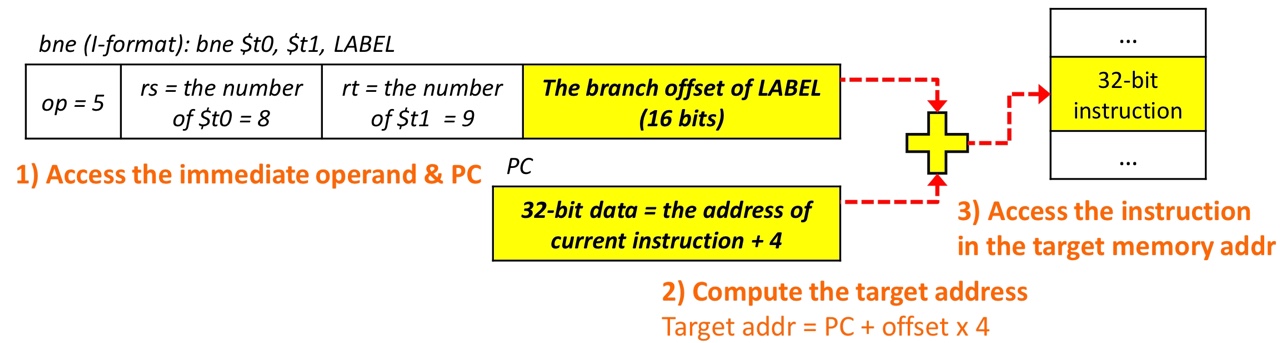
4. PC-relative addressing (with branch instructions)

there is no base address like data transfer instructions
Assumption: most branch targets are near from the current instruction
In HW implementation, PC is already incremented by 4 before computing the current instruction

- PC points next instructions

all instructions are stored in an address that is a multiple of 4.

- by alignment restrictions, it ends with last 2 bits 00

- it increments by 4 which is 00

- it always ends with 00

to save space, MIPS does not store last 2 bits

- to calculate offset, we have to multiply by 4

- actually it can represent up to 18 bits

- 18 bits can represent from PC-2 $^{17}$ to PC+2 $^{17}$ -4

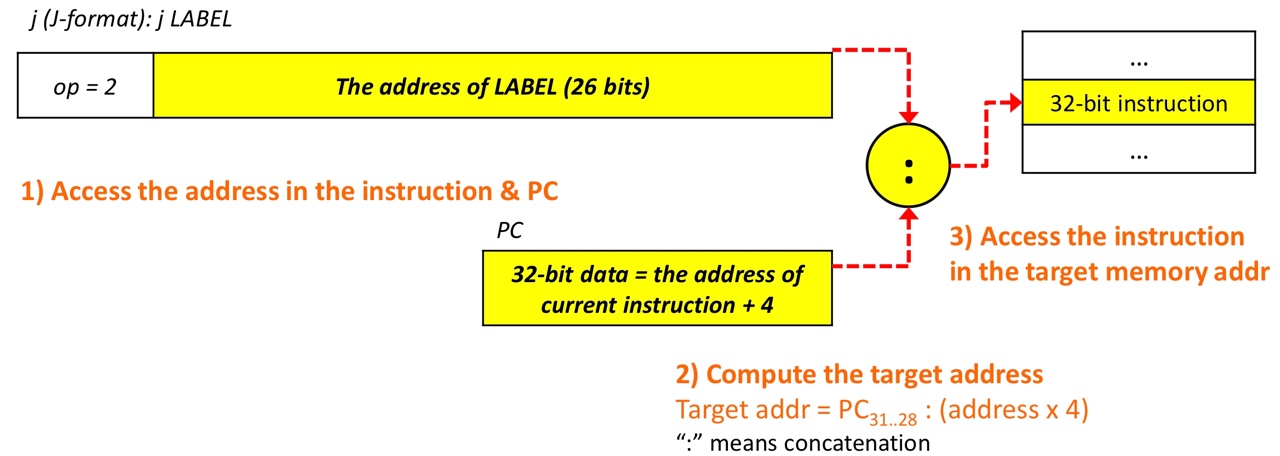
5. Pseudo-direct addressing (with branch instructions)

if branch targets are far from the current instruction (over 16 bits)
last 26 bits are used to represent the address of label
skip last 2 bits like PC-relative addressing

- actually it can represent up to 28 bits

code is stored from 0040 0000 $_{hex}$ to 1000 0000 $_{hex}$

- 1000 0000 $_{hex}$ = 0001 0000 0000 0000 0000 0000 0000 0000 $_{2}$

- which means that we have to access up to 0000 1111 1111 1111 1111 1111 1111 1100 $_{2}$

- always start with 0000 $_{2}$ and end with 00 $_{2}$

- other 26 bits is important

So, with 26 bits we can represent up to 28 bits and concatenate 0000 $_{2}$ to the front